あいさつ
114514810
自己紹介しなくても書いてるの大体ガナリヤなので、要らない気がしてきた・・・
今日はとことんやる気が出ないので、AGCまで時間つぶしに今後のTNP競プロ支部の展望とか書こうかなと思ってます
あと一週間で春休みが終わり、このぐうたらな毎日が終わって、毎日研究と考えると・・・
競プロ支部って?
競プロ支部って何ぞってなるお気持ちになるので説明します。
我々TNPでは主にゲーム制作やイラストを書いたり、音楽制作などを行うのが主な活動ですが、最近は色々なツール・言語の増加によって、これまでよりも幅が広がった活動内容になってきました。
最近勢力を増しているSiv3D支部や、3Dやクオリティの高い2Dを作るUnity支部。
そして、去年の2~4月頃に幾人かで構成された競プロ支部が発足しました。(といっても、ガナリヤが勝手にそう読んでるだけですが・・・
現在は三年生が約3人? と一年生が1人で構成されています?(疑問系なのは、特に競プロ支部集まれ!ってやっていないのとで・・・)
そもそも競プロってなんだよ(哲学)
競プロってなんなんだろう・・・
自分でもたまに迷いますねこれ・・・
競プロは「競技プログラミング」の略で、与えられた問題を制限時間以内に解いてコーディングし、それを提出するやつです。
上のスライドとかが競技プログラミングを物語っている資料でこれを書いた人はすごい人で、競プロ界隈だと知らない人はいません。
例えば、以下の問題を考えてみましょう。
https://yukicoder.me/problems/no/800
問題文 (四平方定理)
上記の問題の$N$, $D$は問題から与えられます。
$(x,\ y,\ z,\ w) = (1, 1, 1, 1), (1, 1, 2, 2), (1, 1, 3, 3), (1, 2, 1, 2), (1, 3, 1, 3), (2, 1, 1, 2), (3, 1, 1, 3)$
勘の良い方、またはプログラミングをした人なら全探索すればいい
と思うと思います。
但し、この問題は
全探索をすると、これの計算量は$(2*10^3)^4 = 8*10^{12}$です。
全探索すると$44$時間かかってしまう計算をするわけにはいきません。
以下、解法です。
$x, y$を全探索することを考えてみます。
$2$つめの式を変形すると
このようにすると、$w, z$を全探索して、$T$という計算結果になるような個数を保存すれば良さそうとなります。
あとは、この$w, z$の計算を先に前計算しておき、その後、$x, y$を計算しておけば、これは計算量は$O(N^2)$に抑えることができ、ACを貰うことができます。
using LL = long long;
//~~~~~~~~~~~~~~~~~~~~~_(^~^ 」 ∠)_~~~~~~~~~~~~~~~~~~~~~
int main() {
int N, D;
cin >> N >> D;
int base = 100000000 / 2;
vector<int> cnt(100000000, 0);
for (int w = 1; w <= N; w++) {
for (int z = 1; z <= N; z++) {
cnt[base + w * w - z * z]++;
}
}
int ans = 0;
for (int x = 1; x <= N; x++) {
for (int y = 1; y <= N; y++) {
int d = x * x + y * y - D;
ans += cnt[base + d];
}
}
cout << ans;
return 0;
}
競技プログラミングは以上のように、まず3つのパートに分かれます。
まず、問題を読むパートです。Writerがどのようなことをさせたいのかを出来るだけ早く読み取ります。
そして、次に考察パートです。ここが苦しいところです。
そして、もし考察が出て解法が生えたら、それを実装する必要があります。
この、「考察が出来る」と「実装が出来る」が別なのが難しいところで、
数学オリンピックなどでは、この考察が出来るパートが要求され、さらに競技プログラミングではここに「プログラミング」の要素が追加されるわけです。
先程の問題と、解法を読んでピンと来る人は少ないだろうなと思います。
でも練習次第で、ある程度は解けるようになります。
競プロのメリット・デメリットって何?
最近情報業界でかなり人気になってきている競技プログラミングですが何が楽しく、何がメリットなのでしょう・・・
自分もたまに、やっぱつれぇわ・・・ってなりながら競技プログラミングをしています。
メリット
競プロを通して得られることは多いです。
まずは、「実装能力 」が挙げられると思います。
次に、考察力 があがると思います。
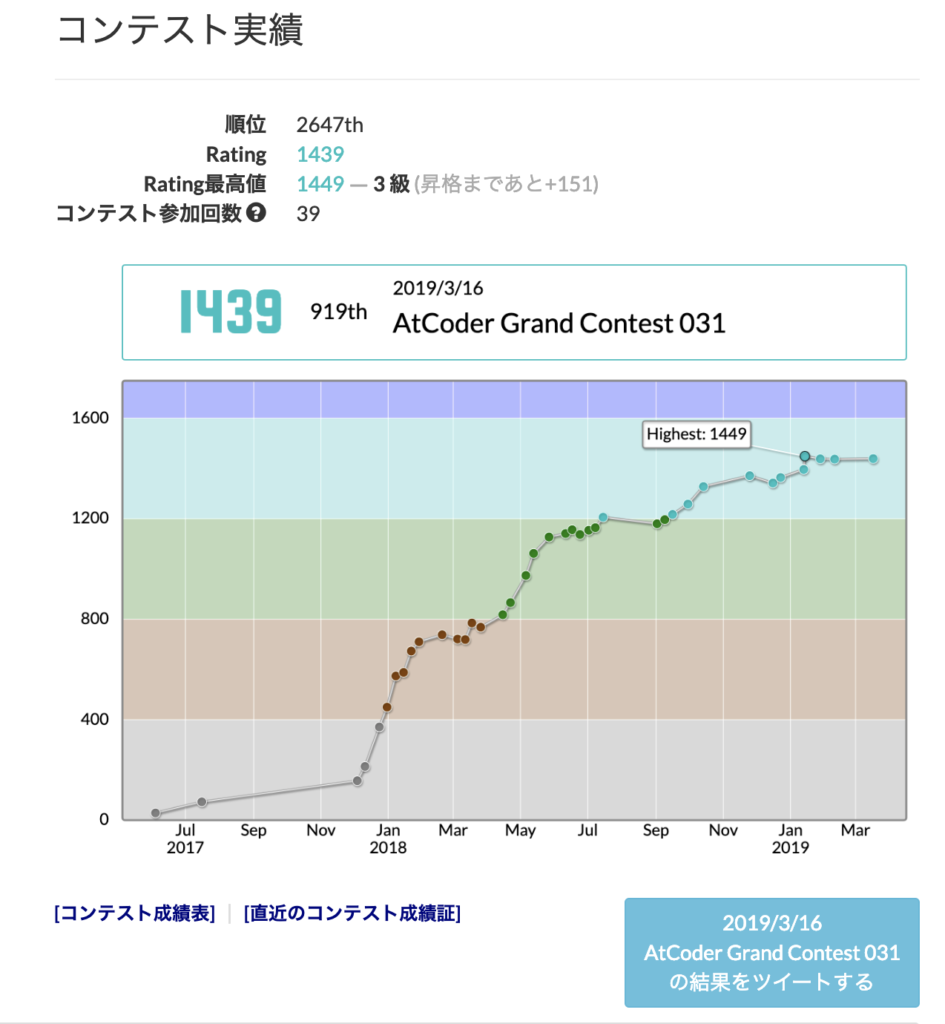
そして、レートが出て、客観的に自分の実力がわかる があると思います。
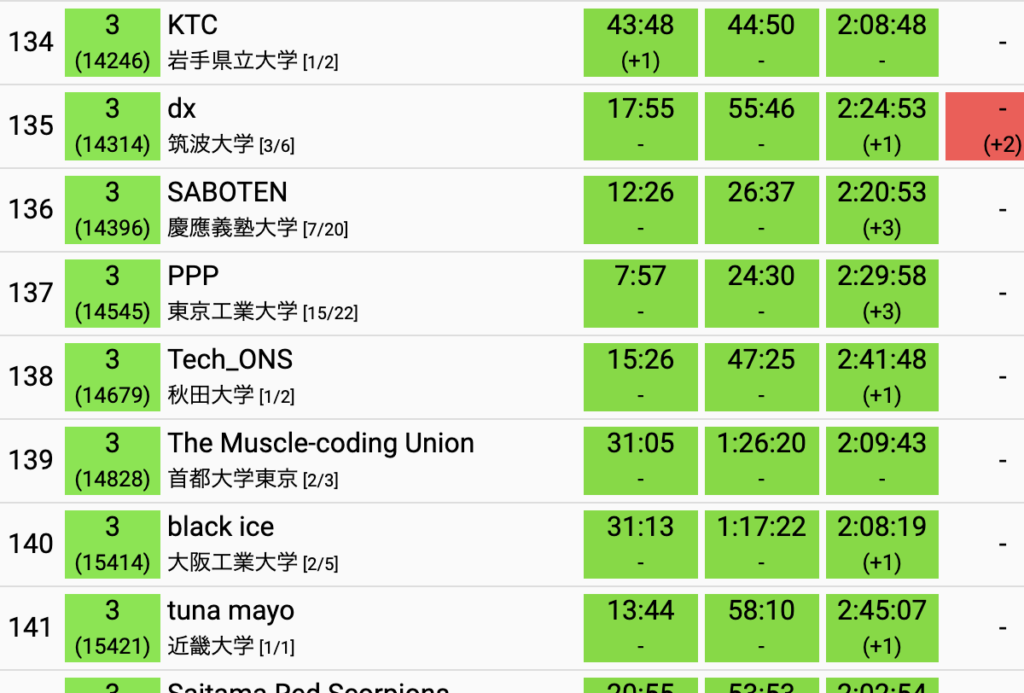
以上は自分のAtCoderでのレート推移です。
でも、だからこそ、練習をして色んなアルゴリズムを覚えて、レートがあがり、初めて400点の問題をコンテスト中に解けたときは、人生でかなり楽しかった瞬間に入ります。
やはり楽しい!!!!!!!
デメリット
デメリットも色々とあります。
まず、「アプリ開発やフレームワークの知識はつかない」
ただ、アプリ開発出来て競プロ出来ない人は見かけますが、競プロ出来てアプリ開発出来ない人はほとんどいないです。
2つ目に、競プロで生活をかなり支配されます。
Codeforcesというサイトはロシアで運営されているコンテストであり、深夜12:35から二時間ぐらいあります。
また、たぴ〜〜〜や、AC、tourist語録など、競プロ用語に支配される日が来ます。
競プロに向く人・向かない人
競プロですが、誰しもに向いているものではないです。
競プロが好きな人はいかのようなことが好きな傾向にあります。
人と争うのが好き 承認欲求が強い 数学・アルゴリズムが好き 順位が好き(レートが好き) 考えることが好き(パズルが好き) 快感を欲している 自分が好き アプリ開発などの長期的スパンが続かない ツイッターが好き 音ゲーがすき(音ゲーマーみんな競プロ強いんですがなぜ・・・) 特に、アプリ開発などの長期的スパン開発が続かない人には向いてますね・・・
競プロが好きでない人は個人的に以下のようなものがある気がします
順位をあまり気にしない 承認欲求が少ない 上昇志向がない 数学・アルゴリズムよりも、開発でプロダクトを作るのが好き 短い努力を繰り返すより、長い努力をしたい アプリ開発が好き
結構、好きな人と好きでない人は正反対の位置にある気がしています。
やりたいことがない人は競プロを始めてみるといいかもしれません。
去年一年の活動について
去年一年、競プロ支部では基本的に個人活動でした。
ただ、去年7月に行われたICPCというチーム大学対抗競プロ大会で
TNPの三年次かつ、同じバイト先の自分含む計三名でICPCインターネット予選に参加し、色々な奇跡が重なってアジア大会に出られることになり、去年の12月に参加しました。
これまでの人生で一番満たされた3日間だったと思います。
4月からの一年の展望
競プロ支部はどのようになっていくのでしょうか・・・
現在、現一年生(新二年生)の一人が昨年から競プロを始めており、競プロが広まって嬉しいなぁというお気持ちになっています。
これからどんどん、新一年生にも広まって、ゲーム開発もできて、競技プログラミングもできる学生が増えればいいなと思っています。
とりあえず今年の7月のICPCに向けて日々精進して行きたいです。
まずはそこからはじめて、普通の国立の中では、秋田大学が競技プログラミングである程度強い大学と言えるように頑張っていこうと思います。
あと、にじさんじの卯月コウってやつエモいから見てくれよな(後方
追伸
どんどんブログを、新入生歓迎に向けて活性化させていきたいお気持ち
みんな書いて♡俺も書いたんだからさ・・・(いやです・・・)